티스토리 뷰
https://www.acmicpc.net/problem/1035
1035번: 조각 움직이기
최대 5개의 조각이 있는 5×5 크기의 보드가 있다. 김지민은 조각을 적절히 움직여서 모든 조각이 연결 요소를 이루게 하려고 한다. 즉 상하좌우로 인접한 조각을 모두 연결했을 때, 모든 쌍의 조
www.acmicpc.net
풀이
0) 주어진 조각의 총 개수를 구한다.
1) 조각의 총 개수로 만들수 있는 모든 경우를 구한다.(DFS)
2) 위의 경우 중 모든 조각들이 이어져 있는 경우를 구한다.
2-1) 임의의 조각 하나에서 BFS. (이어진 조각들의 개수 == 총 조각의 개수) 인 경우 모든 조각이 이어져있는 것이다.
3) 원본에서 2)의 경우로 옮기는 최소 비용을 구한다.
3-1) 이때 이동의 기준은 가장가까운 + 빈 자리 이다.
4) 3)의 최솟값을 갱신한다.
주의사항
1) 어떻게 머리를 잘굴리면 규칙이 있지 않을까?? 하면서 시간낭비 하지말고 걍 완탐하자.
package com.baekJoon;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.StringReader;
import java.util.LinkedList;
import java.util.Queue;
public class BJ_G1_1035_조각움직이기 {
static BufferedReader input = new BufferedReader(new InputStreamReader(System.in));
static int N=5, totalPiece, temp[][], minMove = Integer.MAX_VALUE;
static char origin[][];
static boolean isVisited[][], isOccupied[][];
public static void main(String[] args) throws IOException {
input = new BufferedReader(new StringReader(src));
origin = new char[N][N];
temp = new int[N][N];
for(int r=0; r<N; r++){
String line = input.readLine();
for(int c=0; c<N; c++){
origin[r][c] = line.charAt(c);
if(origin[r][c] == '*'){
totalPiece++;
}
}
}
dfs(0, 0);
System.out.println(minMove);
}
private static void dfs(int idx, int count) {
if(count == totalPiece){
checkLinked();
return;
}
if(idx >= N*N){
return;
}
int r = idx / N;
int c = idx % N;
temp[r][c] = 1;
dfs(idx+1, count+1);
temp[r][c] = 0;
dfs(idx+1, count);
}
private static void checkLinked() {
int sr = 0, sc = 0;
outer : for(int r=0; r<N; r++){
for(int c=0; c<N; c++){
if(temp[r][c] == 1){
sr = r;
sc = c;
break outer;
}
}
}
int cnt = 0;
Queue<Node> queue = new LinkedList<>();
queue.offer(new Node(sr, sc));
isVisited = new boolean[N][N];
isVisited[sr][sc] = true;
while(!queue.isEmpty()){
Node front = queue.poll();
cnt++;
for(int d=0; d<4; d++){
int nr = front.r + dr[d];
int nc = front.c + dc[d];
if(isIn(nr,nc) && !isVisited[nr][nc] && temp[nr][nc] == 1){
queue.offer(new Node(nr, nc));
isVisited[nr][nc] = true;
}
}
}
if(cnt == totalPiece){
int move = getMinMove();
if(minMove > move){
minMove = move;
}
}
}
private static int getMinMove() {
isOccupied = new boolean[N][N];
int sum = 0;
for(int r=0; r<N; r++){
for(int c=0; c<N; c++){
if(origin[r][c] == '*'){
sum += getDist(r, c);
if(sum >= minMove){
return Integer.MAX_VALUE;
}
}
}
}
return sum;
}
private static int getDist(int r, int c) {
isVisited = new boolean[N][N];
Queue<Node> queue = new LinkedList<>();
queue.offer(new Node(r, c, 0));
isVisited[r][c] = true;
while (!queue.isEmpty()) {
Node front = queue.poll();
if(temp[front.r][front.c] == 1 && !isOccupied[front.r][front.c]){
isOccupied[front.r][front.c] = true;
return front.d;
}
for(int d=0; d<4; d++){
int nr = front.r + dr[d];
int nc = front.c + dc[d];
if(isIn(nr, nc) && !isVisited[nr][nc] && !isOccupied[nr][nc]){
queue.offer(new Node(nr, nc, front.d+1));
isVisited[nr][nc] = true;
}
}
}
return 111111;
}
static class Node{
int r;
int c;
int d;
public Node(int r, int c) {
this.r = r;
this.c = c;
}
public Node(int r, int c, int d) {
this.r = r;
this.c = c;
this.d = d;
}
}
static int dr[] = {0,0,-1,1};
static int dc[] = {-1,1,0,0};
static boolean isIn(int r, int c){
return (r>=0 && c>=0 && r<N && c<N);
}
static String src =
".....\n" +
".....\n" +
".**..\n" +
".*...\n" +
"**...";
}
후기
문제를 풀면서 가장 머리굴린 부분은 조각들이 처음부터 붙어 있는 경우이다.
예를들어 아래의 경우

조건을 만족하려면 왼쪽에서 오른쪽이 되어야 한다.

당연히 정답은 2 이다.
하지만 내가 짠 코드의 로직은 가장 가까운 빈자리로 가야하므로 이미 자리를 차지하는 1, 2, 3은 움직이지 말아야 한다.
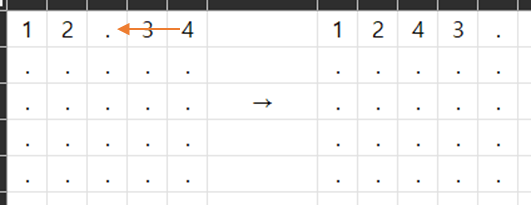
그러면 이렇게 4가 빈자리로 이동해야하는데 여기서 4번이 3번 자리를 밟고 지나가는 것과 3, 4가 나란히 이동하는 최소 거리는 같다. 비슷한 다른경우도 마찬가지이다.
따라서 이미 자리가 차있더라도 밟고 지나갈 수 있도록 새로운 배열 isOccupied 를 만들어서 해결하였다.
'Algorithm' 카테고리의 다른 글
| [백준] G1 2042 구간 합 구하기 (java) (3) | 2023.05.30 |
|---|---|
| [백준] G1 1113 수영장 만들기 (java) (0) | 2023.05.23 |
| [백준] G5 1107 리모컨 (java) (0) | 2021.08.23 |
| [백준] S5 2751 수 정렬하기 2 (java) (0) | 2021.08.22 |
| [백준] G4 20058 마법사 상어와 파이어스톰 (java) (0) | 2021.08.22 |
- Total
- Today
- Yesterday
- 코딩새내기
- SWEA
- 우선순위큐
- G5
- 백트래킹
- java
- BFS
- 리액트
- laugh4mile
- 백준
- PriorityQueue
- 문자열
- map
- S2
- S3
- g4
- 객체지향
- react native
- 시뮬레이션
- 리액트 네이티브
- 현꾸라지
- react
- 다익스트라
- 구현
- DFS
- 자바
- 그리디
- Spring Boot
- Spring
- 알고리즘
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
